Multivariate analysis of variance

Multivariate analysis of variance (MANOVA) is a statistical test procedure for comparing multivariate (population) means of several groups. Unlike ANOVA, it uses the variance-covariance between variables in testing the statistical significance of the mean differences.

It is a generalized form of univariate analysis of variance (ANOVA). It is used when there are two or more dependent variables. It helps to answer : 1. do changes in the independent variable(s) have significant effects on the dependent variables; 2. what are the interactions among the dependent variables and 3. among the independent variables.^[1]

Where sums of squares appear in univariate analysis of variance, in multivariate analysis of variance certain positive-definite matrices appear. The diagonal entries are the same kinds of sums of squares that appear in univariate ANOVA. The off-diagonal entries are corresponding sums of products. Under normality assumptions about error distributions, the counterpart of the sum of squares due to error has a Wishart distribution.

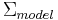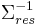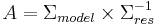Analogous to ANOVA, MANOVA is based on the product of model variance matrix, $\Sigma_{model}$ and inverse of the error variance matrix, $\Sigma_{res}^{-1}$ , or $A=\Sigma_{model} \times \Sigma_{res}^{-1}$ . The hypothesis that 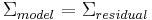$\Sigma_{model} = \Sigma_{residual}$ implies that the product 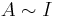$A \sim I$ ^[2] . Invariance considerations imply the MANOVA statistic should be a measure of magnitude of the singular value decomposition of this matrix product, but there is no unique choice owing to the multi-dimensional nature of the alternative hypothesis.

The most common^[3]^[4] statistics are summaries based on the roots (or eigenvalues) 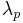$\lambda_p$ of the $A$ matrix:

Samuel Stanley Wilks' 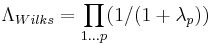$\Lambda_{Wilks} = \prod _{1...p}(1/(1 %2B \lambda_{p}))$ distributed as lambda (Λ)
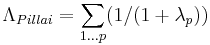
the Pillai-M. S. Bartlett trace, $\Lambda_{Pillai} = \sum _{1...p}(1/(1 %2B \lambda_{p}))$
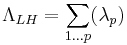
the Lawley-Hotelling trace, $\Lambda_{LH} = \sum _{1...p}(\lambda_{p})$
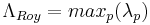
Roy's greatest root (also called Roy's largest root), $\Lambda_{Roy} = max_p(\lambda_p)$

Discussion continues over the merits of each, though the greatest root leads only to a bound on significance which is not generally of practical interest. A further complication is that the distribution of these statistics under the null hypothesis is not straightforward and can only be approximated except in a few low-dimensional cases. The best-known approximation for Wilks' lambda was derived by C. R. Rao.

In the case of two groups, all the statistics are equivalent and the test reduces to Hotelling's T-square.

References

^ Stevens, J. P. (2002). Applied multivariate statistics for the social sciences. Mahwah, NJ: Lawrence Erblaum.
^ Carey, Gregory. "Multivariate Analysis of Variance (MANOVA): I. Theory". http://ibgwww.colorado.edu/~carey/p7291dir/handouts/manova1.pdf. Retrieved 2011-03-22.
^ Garson, G. David. "Multivariate GLM, MANOVA, and MANCOVA". http://faculty.chass.ncsu.edu/garson/PA765/manova.htm. Retrieved 2011-03-22.
^ UCLA: Academic Technology Services, Statistical Consulting Group.. "Stata Annotated Output -- MANOVA". http://www.ats.ucla.edu/stat/stata/output/Stata_MANOVA.htm. Retrieved 2011-03-22.

External links

SFSU Manova page

Statistics

Descriptive statistics

Continuous data

Location	Mean (Arithmetic, Geometric, Harmonic) Median Mode

Dispersion	Range Standard deviation Coefficient of variation Percentile Interquartile range

Shape	Variance Skewness Kurtosis Moments L-moments

Count data

Index of dispersion

Summary tables

Dependence

Statistical graphics

Data collection

Designing studies	Effect size Standard error Statistical power Sample size determination

Survey methodology	Sampling Stratified sampling Opinion poll Questionnaire

Controlled experiment	Design of experiments Randomized experiment Random assignment Replication Blocking Factorial experiment Optimal design

Uncontrolled studies	Natural experiment Quasi-experiment Observational study

Statistical inference

Statistical theory	Sampling distribution Sufficient statistic Meta-analysis

Bayesian inference	Bayesian probability Prior Posterior Credible interval Bayes factor Bayesian estimator Maximum posterior estimator

Frequentist inference	Confidence interval Hypothesis testing Likelihood-ratio

Specific tests	Z-test (normal) Student's t-test F-test Pearson's chi-squared test Wald test Mann–Whitney U Shapiro–Wilk Signed-rank Kolmogorov–Smirnov test

General estimation	Bias Robustness Efficiency Maximum likelihood Method of moments Minimum distance Density estimation

Correlation and regression analysis

Correlation	Pearson product-moment correlation Partial correlation Confounding variable Coefficient of determination

Regression analysis	Errors and residuals Regression model validation Mixed effects models Simultaneous equations models

Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression

Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust

Generalized linear model	Exponential families Logistic (Bernoulli) Binomial Poisson

Partition of variance	Analysis of variance (ANOVA) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical, multivariate, time-series, or survival analysis

Categorical data	Cohen's kappa Contingency table Graphical model Log-linear model McNemar's test

Multivariate statistics	Multivariate regression Principal components Factor analysis Cluster analysis Copulas

Time series analysis	Decomposition (Trend, Stationary process) ARMA model ARIMA model Vector autoregression Spectral density estimation

Survival analysis	Survival function Kaplan–Meier Logrank test Failure rate Proportional hazards models Accelerated failure time model

Applications

Biostatistics	Bioinformatics Biometrics Clinical trials & studies Epidemiology Medical statistics

Engineering statistics	Chemometrics Methods engineering Probabilistic design Process & Quality control Reliability System identification

Social statistics	Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics

Spatial statistics	Cartography Environmental statistics Geographic information system Geostatistics Kriging

Category
Portal
Outline
Index

Design of experiments

Scientific Method	Scientific experiment · Statistical design · Control · Internal & external validity · Experimental unit · Blinding Optimal design: Bayesian · Random assignment · Randomization · Restricted randomization · Replication versus subsampling · Sample size

Treatment & Blocking	Treatment · Effect size · Contrast · Interaction · Confounding · Orthogonality · Blocking · Covariate · Nuisance variable

Models & Inference	Linear regression · Ordinary least squares · Bayesian Random effect · Mixed model · Hierarchical model: Bayesian Analysis of variance (Anova) · Cochran's theorem · Manova (multivariate) · Ancova (covariance) Compare means · Multiple comparison

Designs: Completely Randomized	Factorial · Fractional factorial · Plackett-Burman · Taguchi Response surface methodology · Polynomial & rational modeling · Box-Behnken · Central composite Block · Generalized randomized block design (GRBD) · Latin square · Graeco-Latin square · Hyper-Graeco-Latin square · Latin hypercube Repeated measures design · Crossover study · Randomized controlled trial · Sequential analysis · Sequential probability ratio test

Glossary · Category · Statistics portal · Statistical outline · Statistical topics

Multivariate analysis of variance

References

See also

External links